Теоретико-множественный подход к изучению понятия числа

Статьи о педагогике » Различные подходы к формированию понятия "число" в начальном курсе математики » Теоретико-множественный подход к изучению понятия числа

Страница 2

Учитывая это обстоятельство, в процессе обучения нужно стремиться к тому, чтобы усвоение последовательности соответствующих числительных всегда несколько опережало ту область чисел, которая рассматривается в данный момент основательно.

Приступая к изучению первых десяти чисел, дети должны уже к этому времени более или менее уверено знать названия этих чисел, порядок их следования при счете. Забегание вперед создает условие для переноса изученных операций (операции счета предметов, присчитывание и отсчитывание по 1 и другие) на несколько расширенную область чисел. Это очень важно в качестве психологической подготовки детей к работе с большими числами.

В упражнениях, направленных на усвоение последующих чисел в натуральном ряду, специальное внимание приходится уделять гибкости в ее усвоении. Известно, что дети испытывают затруднения воспроизвести эту последовательность в обратном порядке, при выполнении заданий, требующих умений назвать ряд натуральных чисел, начиная с любого заданного, назвать число, непосредственно ему предшествующее. В результате изучения нумерации чисел дети должны не только усвоить соответствующие общие положения, но и овладеть важнейшими умениями и навыками. В учебниках математики для начальных классов намечена система упражнений, необходимых для сознательного усвоения детьми всех основных вопросов, связанных с изучением натурального ряда чисел.

В изучении нумерации чисел в пределах 10 выделяют подготовительную работу и ознакомление с соответствующими числами.

В подготовительный период, который длится в течение первой учебной недели, выполняются упражнения следующих видов:

1) счет предметов;

2) сравнение групп предметов;

3) знакомство с количественными и порядковыми значениями чисел;

4) рассмотрение порядковых отношений чисел;

5) рисование бордюров;

6) оперирование группами предметов.

На первой неделе занятий дети учатся работать со счетным материалом, с книгой. На этих уроках должно быть отработано умение вести счет различных объектов, при котором используются числа натурального ряда в пределах 10. дети должны усвоить, что, отвечая на вопрос «Сколько?», предметы можно считать в любом порядке, а на вопрос «Который по счету?» – в определенном порядке. Они должны научиться понимать термины «выше», «ниже», «направо», «налево», «справа налево» и т.п., а также выражения, отражающие порядковые отношения: «следовать за», «стоять перед», «находиться между». Дети должны научиться сравнивать две группы предметов. Формирование соответствующих умений и навыков на этих уроках только начинается, оно будет продолжено на уроках по теме «Нумерация». Эти ЗУН необходимы для перехода к изучению нумерации.

Приведем примеры некоторых упражнений, которые формируют эти умения и навыки на данном этапе.

Упражнение 1.

На наборном полотне расположены квадраты разных размеров, красного и синего цвета.

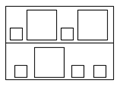
Учитель спрашивает:

- Сколько больших квадратов?

- Сколько маленьких?

- Сколько красных квадратов?

- Сколько желтых?

- Сколько квадратов на верхней полке?

- Сколько на нижней?

- Сколько всего квадратов?

Затем дети сами учатся задавать вопросы, работая по учебнику.

Страницы: 1 2 3 4 5 6 7

Статьи по теме:

Классификация и структура лекций
Существуют классификации лекций по различным основаниям: · месту в лекционном или учебном курсе (вводная, установочная, обзорная, итоговая и др.); · преимущественной форме обучения (лекции при очном, ...

Методические рекомендации по использованию мультимедийного курса «Открытая физика»
Виртуальная лаборатория «Открытая физика» представляет собой пакет программ, оформленный в виде CD-диска и ориентированный на красочную иллюстрацию физических явлений и демонстрацию фундаментальных ф ...

Толковые словари, тезаурус, глоссарий
Словарь Материал из Википедии – свободной энциклопедии Перейти к: навигация, поиск Многотомный латинский словарь. Вот какое определение дают словарю разные источники: Словарь – справочная книга, соде ...

Теоретико-множественный подход к изучению понятия числа

Навигация