Методика изучения темы «Прямоугольник»

Ч.т.д.

Затем ученикам можно предложить систему задач,

направленную на выработку соответствующих умений и навыков.

1. В равнобокой трапеции ABCD углы, прилежащие к стороне AD, равны 45. Найдите высоту трапеции, если основания равны 13 см и 27 см.

2. Докажите, что если в трапеции диагонали равны, то трапеция равнобокая.

3. В трапеции, одно из оснований которой равно 5 см проведена средняя линия, длина которой равна 6 см. Чему равно другое основание трапеции?

4. Диагонали трапеции ABCD пересекают среднюю линию RP в точках М и N. Докажите, что RM=NP.

5. Докажите, что середины сторон равнобокой трапеции являются вершинами ромба.

Конспект урока по теме: «Трапеция. Средняя линия трапеции»

Цели урока.

Образовательные:

закрепит знания изученных свойств трапеции и теорему о средней линии трапеции, научить определять условия существования трапеции; научить применять формулу нахождения средней линии трапеции при решении простейших задач, а также в сходных и новых ситуациях.

Развивающие

: развить навыки самоконтроля и взаимоконтроля, развитие логического мышления, грамотного и аккуратного выполнения работ.

Воспитательные:

воспитание самостоятельности и коллективизма культуры речи.

Оборудование:

2 половины листа и 1 лист копировальной бумаги, каждому ученику письменные принадлежности, лист учёта у каждого ученика.

Ход урока.

1.

Организационный момент урока.

Перед введением определения трапеции полезно вспомнить определение параллелограмма и рассмотреть такой вид четырехугольника, у которого только две противоположные стороны параллельны. (Определение трапеции сопровождается рисунком на доске).

ВС//АD

2. Закрепление понятия трапецииидет через готовые рисунки на доске и вопросы к ним:

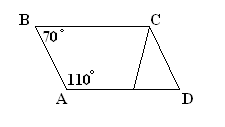
1) Какие четырехугольники на рис. а), б), в) являются трапециями?

Назовите их основания и боковые стороны.

В трапеции МНРК проведен отрезок РЕ//МН. Определите вид четырехугольника МНРЕ.

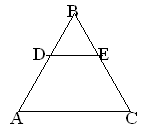
В равностороннем треугольнике АВС со стороной 8 см проведена средняя линия DE. Определите вид четырехугольника АDЕС. Чему равны стороны этого четырехугольника?

Рассмотреть и назвать элементы трапеции, виды трапеции.

Рассмотрение доказательства теоремы о средней линии трапеции.

После изложения доказательства теоремы полезно зафиксировать его этапы:

Дополнительное построение: отрезок ВЕ;

ΔРВС=ΔРЕD.

РО – средняя линия ΔАВЕ.

Вывод: РО//АD, РО= 1/2 (АD+ВС)

Замечание:(РО – средняя линия трапеции, отрезок РО – можно было рассматривать как среднюю линию ΔАВЕ)

4. Первичное закрепление теоремы

о средней линии идет через решение задач типа:

1) Основания трапеции 7 и 9 см. Чему равна средняя линия трапеции?

МN – средняя линия трапеция АВСD. Через т. N проведена прямая, параллельная стороне АВ и пересекает стороны АD в точке Р. Докажите, что МNРА – параллелограмм.

Статьи по теме:

Понятие дети группы риска
Одним из самых важных и в то же время наиболее сложных направлений профессиональной деятельности социального педагога является социально-педагогическая работа с детьми, которых так или иначе всегда в ...

Психологические основы развития звукопроизношенияу детей старшего дошкольного возраста с общим недоразвитием речи
В дошкольном возрасте под влиянием обучения и воспитания происходит интенсивное развитие всех познавательных психических процессов. В этот возрастной период происходит активное сенсорное развитие реб ...

Теоретическая модель спортивной культуры учащихся младших классов
В последнее время в рамках научного, в том числе социологического, исследования спорта все чаще используется понятие "спортивная культура", хотя ему даются различные интерпретации. При всех ...

Навигация

• Главная
• Тенденции современной педагогики
• Спортивно-педагогическая деятельность
• Социализация подростка
• Стандартизация в системе образования
• Связь педагогики с другими науками
• Профессиональное обучение
• Статьи о педагогике