Методика изучения темы «Многоугольники»

Статьи о педагогике » Изучение темы "Многоугольники" в школьном курсе геометрии » Методика изучения темы «Многоугольники»

Страница 3

Учитель обращает внимание учащихся на возможность вписать окружность в правильный многоугольник. Формулируется и доказывается теорема 13.3: «Правильный выпуклый многоугольник является вписанным в окружность и описанным около окружности».

Доказательство теоремы ведется по учебнику. Полезно подчеркнуть, что центры вписанной и описанной окружностей в правильном многоугольнике совпадают и данная точка называется центром многоугольника.

После доказательства теоремы предлагаются задачи:

1.Сторона правильного вписанного в окружность треугольника равна а. Найдите сторону квадрата, вписанного в эту окружность.

Дано: Окружность (0;R),

ΔАВС – правильный, вписанный,

АВ = a,

КМРЕ – вписанный квадрат.

Найти: KM.

Решение.

ΔАВС - правильный, вписанный: R = KMPE - вписанный квадрат в окружность (0;R).

Пусть х =КМ - сторона квадрата, тогда

R = .

Ответ: KM = .

2. В окружность, радиус которой 4 дм, вписан правильный треугольник, на стороне которого построен квадрат. Найдите радиус окружности, описанной около квадрата.

Дано: окружность (0;R),

R=4 дм,

ΔАВС – правильный, вписанный,

Oкр.1 (O;R1),

ABDE – вписанный квадрат в Oкр.1

Найти: R1.

Решение.

1.ΔАВС - правильный, вписанный:

, a=дм.

3. ABDE - вписанный квадрат в Oкр.1 :

R=дм.

Ответ: дм.

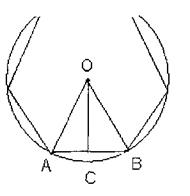
3. Сторона правильного многоугольника равна а, а радиус описанной окружности R. Найдите радиус вписанной окружности. Дано: Окр.(0;R),

A1A2 .An - правильный, вписанный,

A1A2=а, радиус=R,

Окр.(0;г).

Найти: г.

Решение.

ОС - радиус вписанной окружности.

ΔОСВ – прямоугольный (ZC = 90°)

OB=R, СВ=.

ОС2 = ОВ2 - ВС2

ОС=.

Ответ: ОС=.

4.Сторона правильного многоугольника равна а, а радиус вписанной окружности г. Найдите радиус описанной окружности.

Дано: окружность(0;г),

A1A2 .An - пpaвильный., описанный,

А1А2=а, радиус=г,

Окружность (0;R).

Найти: R.

Решение. OB - радиус описанной окружности.

ΔОСВ - прямоугольный (ZC = 90°)

ОС=г, СВ=

ОВ2=ОС2+СВ2

R2=.

Ответ: R = .

Затем учащимся можно предложить систему задач:

1. В правильном шестиугольнике А1А2А3А4А5А6 сторона равна 8. Отрезок ВС соединяет середины сторон А3А4 и А5Аб. Найдите длину отрезка, соединяющего середину стороны А1А2 с серединой отрезка ВС.

2. Сторона правильного шестиугольника ABCDEF равна 32. Найдите радиус окружности, вписанной в треугольник МРК, если М, Р и К -середины сторон АВ, CD. EF соответственно.

3. Выразите сторону b правильного описанного многоугольника через радиус R окружности и сторону а правильного вписанного многоугольника с тем же числом сторон.

4. Периметры двух правильных n-угольников относятся как а:b. Как относятся радиусы их вписанных и описанных окружностей?

5. Сколько сторон имеет правильный многоугольник, каждый из внутренних углов которого равен: 1) 135; 2) 150?

Страницы: 1 2 3

Статьи по теме:

Исследование результативности дифференцированного обучения
При организации дифференцированного обучения в школе встает проблема определения результативности дифференциации. Эта проблема сложная. Что выбрать в качестве показателей результативности дифференциа ...

Особенности использования компьютера в учебном процессе
Стратегия модернизации российского образования предусматривает приоритетность использования новых информационных технологий в учебном процессе, а также усиление практической ориентации и инструментал ...

Роль взрослого в воспитании нравственных качеств у детей старшего дошкольного возраста
Дошкольный возраст – период активного познания мира и человеческих отношений, накопления нравственного опыта, формирования личности. Этот возраст нельзя пропустить для становления представлений о доб ...

Методика изучения темы «Многоугольники»

Навигация