Методика изучения темы «Многоугольники»
В курсе геометрии VI-VIII классов систематически изучаются геометрические фигуры на плоскости, причем большое внимание уделяется многоугольникам, изучению их свойств, рассмотрению величин, характеризующих плоский многоугольник. В решении задач на многоугольники находят применение различные методы.
В различных школьных курсах планиметрии понятие многоугольников трактуется неодинаково.
В одних курсах многоугольник А1, А2, ., Аn трактуется как фигура, состоящая из отрезков A1A2, A2A3, ., An-1An, АnА1 любые два из которых, имеющие общий конец, не лежат на одной прямой (4), (18). В этом случае при рассмотрении площади многоугольников (прямоугольника, параллелограмма, треугольника и др.) под каждым из них понимается соответствующий плоский многоугольник (конечная часть плоскости, ограниченная многоугольником).
В других курсах простой многоугольник (треугольник, четырехугольник и др.) трактуется с самого начала как часть плоскости, ограниченная простой замкнутой ломаной (3).
Выпуклые многоугольники
В учебнике «Геометрия 7-11» Г.П.Бевза (5) «выпуклые многоугольники» рассматриваются в §42 «Многоугольники». Определение «выпуклого многоугольника» дается в конце параграфа: «Если все углы многоугольника меньше развернутого, его называют выпуклым». Затем рассматривается теорема: «Сумма углов выпуклого n-угольника равна 180 (n-2)».
В учебнике «Геометрия 7-11» А.В.Погорелова (18) тема «Выпуклые многоугольники» изучается в §13 «Многоугольники» п. 144.
В начале пункта вводится определение замкнутой: «Ломаная называется замкнутой, если у нее концы совпадают». Затем дается определение многоугольника: «Простая замкнутая ломаная называется многоугольником, если ее соседние звенья не лежат на одной прямой. Вершинами ломаной называются вершинами многоугольника, а звенья ломаной - сторонами многоугольника. Отрезки, соединяющие не соседние вершины многоугольника, называются диагоналями».
После чего рассматривается определение «выпуклого многоугольника»
и доказывается теорема 13.2: Сумма углов выпуклого п-уголъника равна 180(п-2).
В учебнике «Геометрия 7-9» Л.С.Атанасяна (4) тема «Выпуклые
многоугольники» рассматривается в п.40 §1 «Многоугольник» главы 5.
Определение «выпуклого многоугольника» дается в начале пункта: «Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины». Затем рассматривается свойство: «Сумма углов выпуклого n-угольника равна (п-2)180.
Рассмотрим методику изучения темы «Выпуклый многоугольник» на примере учебника геометрии А.В.Погорелова.
При изучении нового материала учащиеся должны познакомиться с несколькими новыми понятиями, уметь дать каждому определение, проиллюстрировать на рисунке.
Классу можно задать вопросы (рисунки к вопросам заготовлены заранее):
1. Назовите концы ломаных А1А2А3А4А5 и B1B2B3B4B5, изображенных на данном рисунке (рис.1).
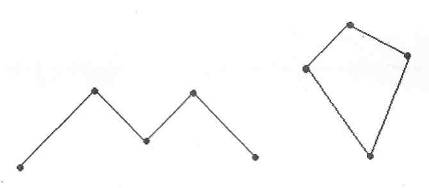
Рис. 1.
2. Чем отличаются друг от друга данные ломаные? [Концы ломаной А1А2А3А4А5 не совпадают, а ломаной B1B2B3B4B5 совпадают].
Дается название ломаной B1B2B3B4B5, - замкнутая ломаная. Составляется определение замкнутой ломаной.
3. Какие из известных фигур можно назвать замкнутыми ломаными? [Треугольник, четырехугольник].
4. Чем отличаются замкнутые ломаные, изображенные на рисунке 2, а, б, от замкнутой ломаной, изображенной на рисунке 2, в? [а) и б) без самопересечения; в) с самопересечением].
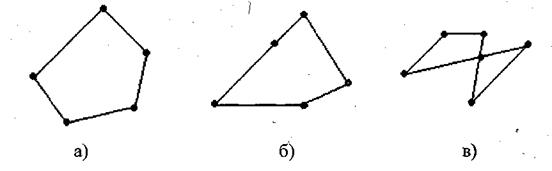
Рис. 2.
5. Чем отличаются друг от друга замкнутые ломаные, изображенные на рисунках 2, а, б? [а) Никакие соседние звенья не лежат на одной прямой].
Дается название: замкнутая ломаная, изображенная на рисунке 2, а, называется многоугольником. Составляется определение многоугольника. Вводятся понятия: вершина, сторона, диагональ.
5. Назовите на рисунке 3 выпуклые четырехугольники. Какой четырехугольник называется выпуклым?
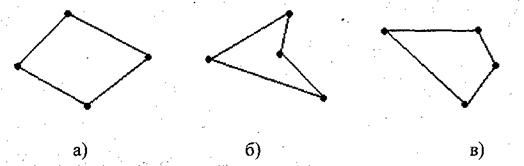
Рис. 3.
7. Составляется определение выпуклого многоугольника: многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону. Вводится понятие угла выпуклого многоугольника: углом выпуклого многоугольника
при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине.
Затем рассматривается теорема 13.2.
Теорема 13.2:
Сумма углов выпуклого п-уголъникаравна 180(п-2).
Дано: A1A2 .An-выпуклый,
п>3.
Доказать: 
A1 + A2 + . + An =180° *(n - 2).
Статьи по теме:
История развития керамических промыслов
«Был я на копанце, был я на топанце, был я на кружале, был я на пожаре, был я на обваре. Когда молод был, то людей кормил, а стар стал, пеленаться стал». Эту загадку в старые годы мог отгадать каждый ...
Взгляды
на участие России в Болонском процессе
Как говорилось выше, у нас в стране есть как противники, так и сторонники реформирования системы образования. Какие же доводы приводят последние за движение реформ в направлении европейских изменений ...
Роль и значение подвижных танцевальных игр для физического
совершенствования дошкольников
Формирование человека на всех этапах эволюционного развития проходило в неразрывной связи с активной мышечной деятельностью, поэтому физические нагрузки приобрели важную биологическую роль в его жизн ...
Навигация
- Главная
- Тенденции современной педагогики
- Спортивно-педагогическая деятельность
- Социализация подростка
- Стандартизация в системе образования
- Связь педагогики с другими науками
- Профессиональное обучение
- Статьи о педагогике