Методы геометрических преобразований

Алгебраический метод решения задач на построении – один из важнейших методов теории конструктивных задач. Именно с помощью этого метода решаются вопросы, связанные с разрешимостью задач тем или иным набором инструментов.

Кроме того, это один из самых мощных методов, позволяющий решать многие задачи, решение которых обычными способами затруднительно. Метод прекрасно демонстрирует тесную взаимосвязь алгебры и геометрии.

Но, к сожалению, в школьном курсе геометрии алгебраическому методу практически не уделяется внимания, хотя с методической точки зрения изучение этого метода не представляет особых сложностей.

Суть метода состоит в следующем:

а) задача сводится к построению некоторого отрезка;

б) используя известные геометрические соотношения между искомыми и данными, составляют уравнение (систему уравнений), связывающее искомые и данные;

в) решая уравнение или систему уравнений, выражают формулой длину искомого отрезка через длины данных;

г) по формуле строится искомый отрезок (если это возможно);

д) с помощью найденного отрезка строится искомая фигура.

Подготовительную работу составляет изучение основных формул и способов построения, где также отрабатываются некоторые элементы схемы решения задач алгебраическим методом, и усваивается сама идея такого подхода к решению задач на построение.

В школьном курсе геометрии обычно рассматривают построения циркулем и линейкой отрезков, заданных следующими некоторыми простейшими формулами:

1) х = а + b (рис. 8).

2) х = а — b(а > b) (рис. 9).

Рис. 8 Рис.9

3) х = nа, где n — натуральное число. Сводится к построению 1). На рис. 10 построен отрезок х, такой, что х = 6а.

Рис. 10 Рис. 11

4) х = .

Строим луч, выходящий из какого-либо конца О данного отрезка а под произвольным углом к нему. Откладываем на этом луче n раз произвольный отрезок b, так что OB = nb (см. рис. 11). Соединяем точку В со вторым концом А отрезка а. Через точку В1, определяемую условием 0В1 = b, проводим прямую, параллельную АВ, и отмечаем точку A1, в которой она пересечет отрезок а.

5) х = а (n и m — данные натуральные числа).

Разделим отрезок а на m равных частей и увеличим полученный отрезок в п раз.

6) х = (построение отрезка, четвертого пропорционального трем данным отрезкам).

Запишем условие в виде пропорции с : а = b : х. Пусть (рис. 12) ОА = а, ОС = с, так что члены одного из отношений отложены на одном луче, исходящем из точки О. На другом луче, исходящем из той же точки, откладываем известный член другого отношения ОB = b. Через точку А проводим прямую, параллельную ВС, и отмечаем точку X ее пересечения с прямой ОВ. Отрезок ОХ искомый, то есть ОХ = х.

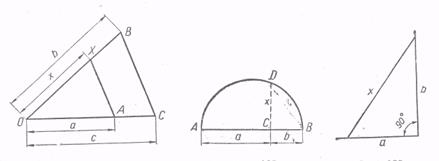
Рис. 12 Рис. 13 Рис. 14

7) x = .

Можно воспользоваться построением 6), полагая b = а.

8) х = (построение среднего пропорционального двух данных отрезков).

Строим отрезки АС = а, ВС = b, так что АВ = а + b. На АВ как на диаметре строим полуокружность (см. рис. 13). В точке С восставим перпендикуляр к АВ и отметим точку D его пересечения с окружностью. Тогда х = CD.

9) х = Отрезок x строится как гипотенуза прямоугольного треугольника с катетами а и b (см. рис. 14).

10) х = (a > b). Отрезок x строится как катет прямоугольного треугольника с гипотенузой а и катетом b.

К рассмотренным построениям можно свести построение отрезков, заданных более сложными формулами.

Желательно постепенное изучение этих формул, когда каждая из них разбирается при рассмотрении теории, необходимой для осуществления соответствующего построения.

Статьи по теме:

Результаты диагностики уровня сформированности творческого мышления у младших подростков
В данном параграфе мы приводим результаты диагностики творческого мышления младших подростков экспериментальной группы (N=15). Для обработки полученных данных нами были использованы качественный и ко ...

Сенсомоторное развитие дошкольников
Прежде чем раскрыть значение сенсомоторного развития для детей старшего дошкольного возраста нам необходимо рассмотреть, что собой представляет сенсорное и моторное развитие детей. Сенсорное развитие ...

Какие требования предъявляются к экономической части дипломного проекта
Во-первых, студент должен продемонстрировать не только знание экономической теории, изученной по книгам и лекциям, а умение творчески использовать эти знания для исследования реальных инженерных проб ...

Навигация

• Главная
• Тенденции современной педагогики
• Спортивно-педагогическая деятельность
• Социализация подростка
• Стандартизация в системе образования
• Связь педагогики с другими науками
• Профессиональное обучение
• Статьи о педагогике