Методика изучения темы «Четырехугольники»
Четырехугольники - традиционный для курса планиметрии материал. Как и треугольник, четырехугольник трактуется в одних учебниках как простая замкнутая четырехзвенная ломаная, в других – как часть плоскости, ограниченная такой ломаной. Из всевозможных четырехугольников выделяют выпуклые. Во всех действующих в настоящее время пособиях осуществляется одинаковый подход во введении частных видов параллелограммов: прямоугольников и ромбов. Квадрат в одних учебниках вводится как четырехугольник, который одновременно является прямоугольником и ромбом. В других квадрат определяется как частный вид прямоугольника. Трапеция рассматривается после параллелограммов.
При установлении различных свойств и признаков параллелограмма широко используются свойства и признаки равных треугольников, свойств углов, образованных при пересечении двух параллельных прямых третьей, признаки параллельности прямых. Материал о параллелограммах и их частных видах очень удобен для формирования и развития логического мышления учащихся. Именно здесь учитель имеет широкие возможности по работе с определениями: предложить, например, ученику дать определение прямоугольника через понятие прямоугольника, параллелограмма и т.д.
В учебнике «Геометрия 7-11» А.В. Погорелова (18) тема «Параллелограмм» изучается в 6 параграфе «Четырехугольники» в трех пунктах.
В п.51 «Параллелограмм» в начале вводится определение параллелограмма: «Параллелограмм - это четырехугольник, у которого противолежащие стороны параллельны, т.е. лежат на параллельных прямых», а затем рассматривают и доказывают признак параллелограмма (Т.6.1).
Теорема 6.1: Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник -параллелограмм.
В п.52 «Свойство диагоналей параллелограмма» и п.53 «Свойство противолежащих сторон и углов параллелограмма» изучаются свойства параллелограмма:
1. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. (Т.6.2, которая является обратной теореме 6.1).
2. У параллелограмма противолежащие стороны равны, противолежащие углы равны. (Т.6.3)
В учебнике «Геометрия 7-9» Л. С. Атанасяна (5) тема «Параллелограмм» рассматривается в §2 «Параллелограмм и трапеция» в пунктах 42 и 43.
Определение и свойства параллелограмма даются в п.42 «Параллелограмм»:
Опр.: Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны. Свойства:
1. В параллелограмме противолежащие стороны и противолежащие углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Л.С. Атанасян выделяет три признака параллелограмма, которые изучаются в 43 пункте «Признаки параллелограмма»:
1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник - параллелограмм.
2. Если в четырехугольнике противолежащие стороны попарно равны, то этот четырехугольник - параллелограмм.
3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм.
Рассмотрим методику изучения темы «Параллелограмм» на примере геометрии А.В. Погорелова. Понятие параллелограмма вводится с помощью таблицы «Четырехугольники».
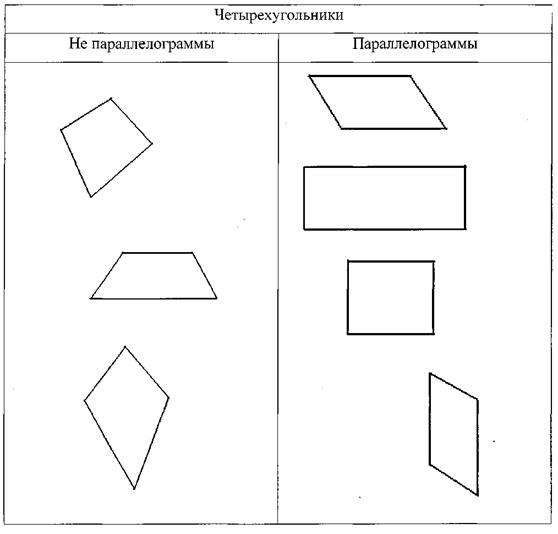
В таблице показаны два вида четырехугольников: параллелограммы и не параллелограммы.
Параллелограмм иллюстрируется не одним объектом, входящим в объем этого понятия, что дает возможность с первого урока учащимся не приписывать этому понятию несущественные признаки: один угол острый, а другой - тупой, стороны не равны и т.д.
Статьи по теме:
Профессиональная консультация
Профессиональная консультация (от лат. profession - род занятий, consultatio - совещание) - научно организованное информирование о профессиях, предназначенное главным образом для молодежи, оканчивающ ...
Толковые словари, тезаурус, глоссарий
Словарь Материал из Википедии – свободной энциклопедии Перейти к: навигация, поиск Многотомный латинский словарь. Вот какое определение дают словарю разные источники: Словарь – справочная книга, соде ...
Развивающие индивидуально-групповые занятия с подростками
осложненного поведения
Взаимодействуя с существующими общественными ценностями в жизни, подросток сравнивает свое поведение с теми образцами, которые предлагаются ближайшим окружением: родителями, педагогами и другими знач ...
Навигация
- Главная
- Тенденции современной педагогики
- Спортивно-педагогическая деятельность
- Социализация подростка
- Стандартизация в системе образования
- Связь педагогики с другими науками
- Профессиональное обучение
- Статьи о педагогике