Методика решения задач на построение

Статьи о педагогике » Решение задач на построение в курсе геометрии основной школы как средство развития логического мышления школьников » Методика решения задач на построение

Страница 3

Хотя доказательство при решении задач на построение проводится аналогично доказательству теорем, с использованием аксиом, теорем и свойств геометрических фигур, между ними имеется и некоторое различие. При доказательстве теорем в большинстве случаев без труда выделяют условие и заключение. При решении задач на построение уже труднее найти данные, на основании которых можно доказать, что построенная фигура является искомой. Поэтому при решении конструктивных задач в классе целесообразно иногда специально выделять, что дано, и что требуется доказать. Например, при решении задачи: “Построить ромб по двум его диагоналям” предлагаем ученику записать, что дано (диагонали взаимно перпендикулярны и, пересекаясь, делятся пополам) и что требуется доказать (стороны равны). В свою очередь при решении задач дома и в контрольных работах можно не требовать оформления доказательства с выделением отдельно условия и заключения. Нет надобности требовать проведения особого доказательства в задачах, где правильность решения очевидна.

При построении обычно ограничиваются отысканием одного какого-либо решения, причем предполагается, что все шаги построения действительно выполнимы. Для полного решения задачи нужно еще выяснить следующие вопросы: 1) всегда ли (то есть при любом ли выборе данных) можно выполнить построение избранным способом; 2) можно ли и как построить искомую фигуру, если избранный способ нельзя применить; 3) сколько решений имеет задача при каждом возможном выборе данных? Рассмотрение всех этих вопросов и составляет содержание исследования.

Таким образом, исследование имеет целью установить условия разрешимости и определить число решений. Нередко школьники и даже учителя проводят исследование, произвольно выбирая те или иные случаи, причем неясно, почему рассматриваются именно такие, а не какие-либо иные случаи. Остается неясным также, все ли возможные случаи рассмотрены. Практически в большинстве случаев удается достигнуть необходимой полноты исследования, если проводить это исследование по ходу построения, что является наиболее доступным и целесообразным способом. Сущность этого приема состоит в том, чтобы перебрать последовательно все шаги, из которых слагается построение, и относительно каждого шага установить, всегда ли указанное на этом шаге построение выполнимо, а если выполнимо, то однозначно ли.

Рассмотрим решение и исследование задачи: “Построить окружность, касающуюся данной прямой PQ и данной окружности (О; ОА) в заданной на ней точке А”.

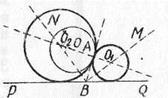
Рис. 2

Решение. Решаем эту задачу методом геометрических мест. Проводим прямую ОА (рис. 2). В точке А строим касательную АВ к данной окружности, а затем — биссектрисы углов РВА и ABQ. Точки пересечения прямой ОА с прямыми ВМ и BN и будут центрами искомых окружностей.

Проводя исследование по построению, легко обнаруживаем, что наше решение не применимо, если OAPQ. Для такого случая рассматриваем решение задачи отдельно. В результате получим, что если ОА не перпендикулярна PQ, то задача имеет два решения, за исключением случая, когда окружность (О; ОА) пересекает PQ в точке А, так как тогда прямые ВМ, ВN и ОА пересекутся в точке А, и окружности не получим. Если же OAPQ, но А не лежит на PQ, то получаем одну окружность с центром на ОА и радиусом, равным половине расстояния от точки А до данной прямой PQ. Если же при этом А лежит на PQ, то задача неопределенная.

Таким образом, для задачи имеются лишь 4 характерные конфигурации исходных данных:

1) ОА не перпендикулярна PQ и А не принадлежит PQ — 2 решения;

2) OA не перпендикулярна PQ и A принадлежит PQ — нет решений;

3) OAPQ, но A не принадлежит PQ — 1 решение;

4) OAPQ и А принадлежит PQ — бесконечное множество решений.

В итоге таких рассуждений решается вопрос о возможности и однозначности построения искомой фигуры данным способом. Но остается еще открытым вопрос: не возникнут ли новые решения, если изменить как-либо способ построения? Иногда удается доказать, что всякое решение данной задачи совпадает с одним из уже полученных решений. Если же это не удается, то можно предположить, что задача имеет другие решения, которые могут быть найдены другими способами. В этих случаях надо тщательно проверить, нет ли каких-либо иных возможных случаев расположения данных или искомых фигур, которые не были предусмотрены ранее проведенным анализом.

Страницы: 1 2 3

Статьи по теме:

Работа с одаренными детьми
Потребность одаренных детей в эмоциональном комфорте очень велика, особенно в признании и осознании собственной цены. Способность детей к большому количеству и смене восприятий порождает и уязвимость ...

Факторы становления самооценки младшего школьника
Самооценку с раннего детства формирует воспитание. Воспитание самооценки в ребенке – одна из самых важных задач для его будущей жизни. Большое значение в становлении самооценки имеет стиль семейного ...

История отношения общества к умственно отсталым и социальная политика РФ в отношении детей с ограниченными возможностями здоровья
На всех этапах своего развития человеческое общество проявляло внимание к людям, имеющим те или иные нарушения физических или психических качеств. Если такие лица оставались без внимания, это станови ...

Методика решения задач на построение

Навигация